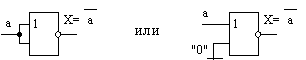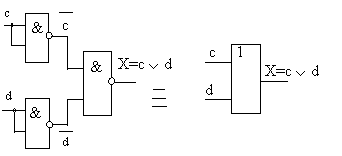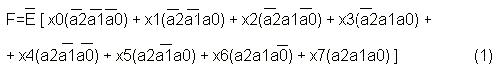СОДЕРЖАНИЕ
1. Лабораторная работа№1 «ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ»
2. Лабораторная работа№2 «ФУНКЦИОНАЛЬНЫЕ СВОЙСТВА ПОЛНЫХ ДЕКОДЕРОВ»
3. Лабораторная работа№3 «МУЛЬТИПЛЕКСОРЫ – СЕЛЕКТОРЫ»
ЛИТЕРАТУРА
1. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
1. Цели лабораторной работы
Исследование функциональных свойств простейших логических элементов, изучение способов описания их работы и применения. Ознакомление с параметрами логических элементов серии ИМС К155 и К1533.
2. Основные сведения и понятия
Логическим элементом называется минимальная совокупность взаимосвязанных компонентов, выполняющая простые логические операции (действия) над входными сигналами. К таким операциям относятся, например, логическое сложение (элемент ИЛИ), логическое умножение (элемент И), отрицание или инверсия (элемент НЕ) и ряд других.
Описать работу логического элемента - это значит выбрать способ задания зависимости его выходного сигнала от входных. А точнее - определить зависимость значений выходного сигнала от значений входных сигналов. Так как входные и выходные сигналы в логических устройствах могут принимать только два значения: логического нуля (лог. 0) и логической единицы (лог. 1), то указанные зависимости будут двоичными.
Для отображения двоичных зависимостей можно использовать три основных способа: табличный, графический и аналитический. Выбор того или иного способа зависит от целевого назначения описания элемента. Если требуется уяснить работу элемента только в установившемся режиме (в статике), то достаточно применить табличный способ - построить таблицу истинности, в которой указать значения выходного сигнала при всех возможных комбинациях (значений) входных сигналов.
Графическое описание работы элемента заключается в построении временных диаграмм, на которых отображаются (в виде условных уровней) значения входных и выходных сигналов и их изменения во времени. Этот способ применяют, когда необходимо оценить быстродействие элемента, либо отобразить форму и длительность сигналов, т.е. отобразить работу элемента в динамике.
Аналитический способ используется для анализа функциональных свойств элемента, поиска возможных вариантов его применения при построении более сложных логических устройств и для формализации условий его работы. Этот способ основан на применении булевой алгебры, с помощью которой выходной сигнал элемента представляется функцией от входных сигналов - аргументов этой функции. Функция обозначается прописными, а аргументы строчными буквами латинского алфавита. Логические же операции - специальными символами. В технических приложениях булевой алгебры логическая сумма обозначается знаком плюс (+), логическое произведение - точкой (.), либо символом (&), а инверсия - чертой над переменной (a) и читается "не а".
Чтобы исследовать функциональные свойства логического элемента, необходимо найти алгебраическое выражение выходной его функции в явном виде, отобразив зависимости логическими символами между входными переменными (аргументами функции). Затем, пользуясь законами и следствиями булевой алгебры, а также определениями логической суммы, произведения и инверсии, сформулировать свойства элемента и определить его назначение.
Рассмотрим это на конкретном примере. Проанализируем функциональные свойства двухвходового логического элемента И-НЕ. Условное графическое обозначение (УГО), таблица истинности и временные диаграммы работы этого элемента приведены на рисунке 1 а, б, в - соответственно.
№ |
Комб вх сигн |
Вых |
Комб |
a |
b |
Х |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
2 |
1 |
0 |
1 |
3 |
1 |
1 |
0 |

Рисунок 1. Этапы анализа функциональных свойств элемента 2И-НЕ
Из УГО элемента следует, что входы элемента потенциальные не инверсные, а выход - инверсный, потенциальный. Обозначим входные сигналы буквами "а" и "b", соответственно по входам "вх 1" и "вх 2", и выходной сигнал - функцией Х.
Примем, что сигнал лог.1 отображается более высоким уровнем, чем сигнал лог.0, см. рис. 1в (такое соглашение называют соглашением "положительной логики"). Тогда, проводя эксперимент, в котором на входы элемента будут подаваться все возможные наборы значений двух сигналов "а" и "b" (комбинации без избыточного двоичного двухэлементного кода), можно определить значения выходного сигнала Х (функции). По результатам эксперимента строится таблица истинности рис 1б. Анализируя таблицу, замечаем, что Х принимает значения лог.0 только в том случае, когда оба входных сигнала (и "а" и "в") имеют значение лог.1 , т.е. сигналы лог.1 совпадают по времени. Поэтому выходной сигнал описывается инверсией логического произведения переменных "а" и "в":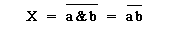 (1)
(1)
Таким образом, элемент И-НЕ (рис. 1а) представляет собой схему совпадения с инверсией входного сигнала.
Обратите внимание: функция (1) была определена по отношению к единичным значениям входных сигналов. Другими словами, если активными значениями входных сигналов считать значение лог.1, то элемент И-НЕ реализует инверсию логического произведения этих сигналов. Если же за активное значение входных сигналов принять низкий уровень (лог. 0), тогда в то же самое время элемент И-НЕ реализует логическую сумму инверсий входных сигналов, т.е.
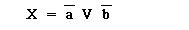 (2)
(2)
и ему будет соответствовать УГО рис.1г.
Анализируя зависимости (1) и (2) при а = в, получим:
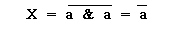 или
или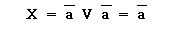 (3)
(3)
Аналогичный результат можно получить приняв b = 1:
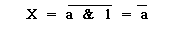 и
и 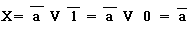 (4)
(4)
Из выражений (3) и (4) следует вывод: элемент И-НЕ можно использовать в качестве инвертора (элемента НЕ), для этого достаточно на оба входа подать один и тот же сигнал, либо один из входов подключить к шине лог.I (Рисунок 2)

Рисунок.2. Реализация элемента НЕ на элементе И-НЕ
Аналогичное утверждение справедливо и для элемента ИЛИ-НЕ. Разница заключается в том, что на свободный вход надо подать логический 0. Реализация элемента Не, для данного случая приведена на рисунке 3.
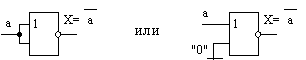
Рисунок.3. Реализация элемента НЕ на элементе И-НЕ
Заметим, что выражения (1) и (2) получены для одного и того же элемента, однако описывают его при различных соглашениях - соглашениях «положительной» и «отрицательной» логики, соответственно.
Очевидно
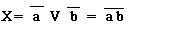 (5)
(5)
Соотношение (5) известно в булевой алгебре, как правило Де Моргана. Из этого соотношения следует вывод: логические элементы И-НЕ позволяют реализовать логическую сумму дискретных сигналов.
Действительно, допустим 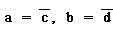 и подставим в выражение (5), тогда:
и подставим в выражение (5), тогда:
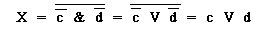 (6)
(6)
Полученному соотношению соответствуют эквивалентные схемы, реализующие логическую сумму сигналов "с" и "d", представленные на рисунке 4.
Учитывая сказанное, нетрудно придти к результирующему выводу о функциональных свойствах элементов И-НЕ: набор элементов И-НЕ позволяет реализовать любое логическое устройство сколь сложно оно ни было и этот набор является функционально полным.
Анализируя работу элемента И-НЕ во времени, строят временные диаграммы (рис.1,в) при конкретной выбранной последовательности входных сигналов, отображая на отдельной диаграмме "Х" значения выходного сигнала в зависимости от значений входных. Так диаграммы рис.1,в иллюстрируют случай, когда входные сигналы "а" и "в" изменяются в последовательности 00-10-11-01-00. Причем длительности фронта и спада этих сигналов исчезающе малы (прямоугольная форма). Момент изменения значений сигналов помечены, соответственно, t0и t2 - для сигнала a; t1и t3 - для сигнала b. Поэтому временные соотношения входных сигналов легко определить:
1. Δt1 = t2 - t0 - длительность сигнала "а";
2. Δt2 = t3 - t1 - длительность сигнала "в"
3. (t1- t0) - задержка по фронту сигнала "в" относительно фронта сигнала "а";
4. (t2- t1) - интервал времени, когда оба сигнала имеют значение лог.I (длительность активного воздействия)
Согласно таблице истинности (рис.I б) только в течение интервала t1÷t2 выходной сигнал "Х" может принять значение лог.0. Но если учесть возможные задержки изменения Х относительно моментов t1 и t2 , то длительность сигнала Х (значение лог.0) будет равна:
Δtх = t2 - t1 + 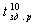 -
- 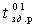 (7)
(7)
В формуле (7)
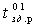 - время задержки распространения сигнала при переходе элемента из состояния лог.0 в состояние лог.I (при "выключении");
- время задержки распространения сигнала при переходе элемента из состояния лог.0 в состояние лог.I (при "выключении");
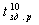 - время задержки распространения сигнала при переходе элемента из состояния лог.I в состояние лог.0 (при "включении").
- время задержки распространения сигнала при переходе элемента из состояния лог.I в состояние лог.0 (при "включении").
Примеры  и
и 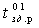 обычно приводятся в справочниках по ИМС [I].
обычно приводятся в справочниках по ИМС [I].
Очевидно, если t2 - t1 ≤ tзд.р,то выходной сигнал не изменит значения лог.I и элемент И-НЕ не будет реагировать на входные сигналы.
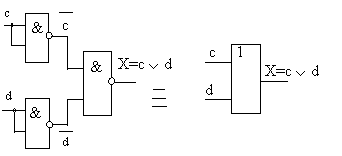
Рисунок 4. Реализация логической суммы на элементах И-НЕ (а), на элементе ИЛИ (б)
3. Описание лабораторной установки
Установка представляет собой учебный стенд с электропитанием от сети переменного тока 220В. f = 50Гц, комплектуемый 6-ю сменными блоками и встроенный блок вторичного электропитания на +5В.
На лицевой панели блока расположены:
- тумблеры для подачи сигналов лог.I и лог.0 на входы используемых логических элементов SAI ÷ SA4 и SA5 ÷ SA8;
- светодиоды HI ... H4 и H5 ... H8 для визуального контроля значений выходных сигналов элементов (горение электрода соответствует сигналу лог.I);
- гнезда для коммутации логических элементов между собой и контроля сигналов с помощью осциллографа.
Для исследования работы элементов в динамическом режиме предусмотрен генератор прямоугольных импульсов и делитель частоты импульсов. Частота импульсов может принимать значения 1мГц и 500кГц. В лабораторной работе исследуются логические элементы ИЛИ, И, ИЛИ-НЕ, И-НЕ исключающие ИЛИ непосредственно реализованные микросхемами: КI55ЛЛI, КI55ЛИI, КI55ЛЕ4, КI55ЛА3, КI55ЛП5 соответственно. Кроме того, можно исследовать схемы, эквивалентные логическим элементам ЗАПРЕТ, ИМПЛИКАТОР и др. реализуемые сборочными операциями на имеющихся элементах.
4. Задание на лабораторную работу
4.1. Уяснить основные понятия и методику анализа функциональных свойств логических элементов. Ознакомиться с конструкцией лабораторного стенда и блоков.
4.2. Каждый логический элемент исследуется в статическом и динамическом режимах работы. При этом необходимо:
- уяснить (составить) УГО элемента при соглашениях положительной и отрицательной логики;
- составить таблицу истинности;
- найти алгебраическое выражение функции, реализуемой элементом;
- построить временные диаграммы работы элемента;
- сделать выводы о свойствах элемента и его применении.
Перечень логических элементов, подлежащих исследованию, их условные графические обозначения при соглашениях положительной логики и наименования приведены в таблице 1. Из логических элементов поз.9-12 (таблицы 1)исследуется только один по указанию преподавателя.
4.3. Для микросхем серии КI55: ЛЛI, ЛИI, ЛЕ4, ЛП5, ЛА3, ознакомиться с их УГО, цоколевкой и электрическими параметрами.
4.4. При выполнении лабораторной работы руководствоваться методическими указаниями п.6.
5.Содержание отчета
Отчет выполняется и оформляется в соответствии с требованиями кафедры АиПУ. В отчете представить:
5.1. УГО исследуемых логических элементов, их цоколевку, таблицы истинности по форме рисунка. I.б, алгебраические выражения реализуемых функций. Данные свести в таблицу по форме таблицы 1.
- Временные диаграммы работы логических элементов в динамическом режиме.
5.3.Выводы по функциональным свойствам элементов и их применению
6. Методические указания
6.1. Для приведения стенда в рабочее состояние необходимо тумблер СЕТЬ на стенде поставить в положение "ВКЛ". Затем проконтролировать наличие напряжений по загоранию светодиода.
6.2. Помните, что на неиспользуемом входе логического элемента будет постоянно сигнал лог.I.
Запрещается выходы элементов соединять с корпусом стенда или гнездом "+". Обращайте на это особое внимание при исследовании собранных схем: запрещается включать тумблер, если соответствующий вход соединен с выходом какого - либо элемента.
6.3. При выполнении задания (п.4.2) руководствуясь методикой анализа, аналогично рассмотренной в п.2 на примере логического элемента И-НЕ. Результаты анализа оформляйте в форме таблицы 1 и рисунком, аналогичным рисунку I. По окончании анализа все графы таблицы, соответствующие ее позициям 1÷8, должны быть заполнены. Дополнительно заполнить графы по заданной преподавателем позиции.
6.3.1. Так как в составе стенда нет ИМС логических элементов, соответствующих поз.7÷12 таблицы 1, то вначале необходимо составить эквивалентные схемы на имеющихся логических элементах, предъявить их для контроля преподавателю, затем собрать и исследовать их работу. Поскольку анализ элемента И-НЕ в данном описании приведен, то целесообразно выполнить эксперименты и убедиться в справедливости изложенных выводов.
Все УГО логических элементов, приводимые в отчете и формируемые в процессе выполнения лабораторной работы, должны соответствовать требованиям ГОСТ 2.743-82 [2]. Чтобы сформировать УГО какого-либо логического элемента, необходимо найти алгебраическое выражение реализуемой этим элементом функции. Правила формирования легко уяснить, сопоставляя рис.1, а с выражением (I) и рис. I,г с выражением (2) для функции И-НЕ.
Заметим, что сопоставляя левую и правую части соотношения (6) со схемой рисунок 4,а и УГО рисунок 4,б,соответственно, нетрудно сформировать УГО элемента ИЛИ в отрицательной логике.
И вполне очевидно, что по УГО элемента достаточно просто записать алгебраическое выражение выходной функции. Учтите это при анализе элементов позиции 7÷12, таблицы 1.
6.3.2. Анализ работы логического элемента в динамическом режиме провести с учетом тех последовательностей сигналов, которые можно получить в лабораторной установке. При этом руководствуйтесь диаграммами, приведенными на рисунке 1 в. Необходимо выбрать такую последовательность входных сигналов, чтобы выходной сигнал исследуемого логического элемента изменял свое значение, и этот случай отобразить на временных диаграммах.
Построив временные диаграммы, убедиться в их верности, поставив эксперимент. Для этого составьте схему эксперимента, соберите ее на стенде и с помощью осциллографа пронаблюдайте осциллограммы входных и выходных сигналов. Учтите, что быстродействие ИМС КI55 достаточно велико (задержки 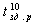 и
и 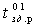 составляют порядка нескольких десятков наносекунд), поэтому соответствующим образом выберете скорость развертки осциллографа, длительность и частоту импульсов сигнала.
составляют порядка нескольких десятков наносекунд), поэтому соответствующим образом выберете скорость развертки осциллографа, длительность и частоту импульсов сигнала.
Измерьте с помощью осциллографа длительности импульсов на выходах генератора и делителя частоты. Отобразите эти данные на временной диаграмме.
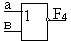
Таблица 1 Логические элементы исследуемые в лабораторной работе.
№ |
УГО элемента
(соглашение положительной логики) |
Наименование
Элемента |
УГО элемента
(соглашение отрицательной логики) |
Алгебраич.
выражение реализуемая
функции |
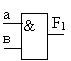
| 1. |
|
2И
(схема
совпадения) |
|
|
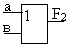
| 2. |
|
2ИЛИ
(схема
совпадения) |
|
|
| 3. |

|
НЕ
(инвертор) |
|
|
| 4. |
|
2ИЛИ-НЕ |
|
|
| 5. |
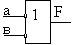
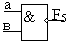 |
2И-ИЛИ
(элемент
Шеффера) |
а |
F5=ав=а+в |
6. |
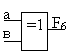
|
Исключающее
ИЛИ |
|
|
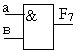
7. |
|
Запрет |
|
|
8. |

|
Импликатор |
|
|
9. |

|
2И-ИЛИ |
|
|
10.
|
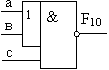
|
2ИЛИ-2И-НЕ |
|
|
11.
|
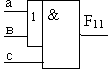
|
2ИЛИ-2И |
|
|
12.
|
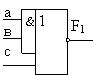
|
2И-2ИЛИ-НЕ |
|
|
7. Вопросы для самопроверки
1. Какие минимальные базисы существуют?
2. Каким образом перейти из базиса в базис?
3. Какой элемент называется функционально полным и каковы способы доказательства полноты логического элемента?
4. Что означают термины: «соглашение положительной логики» и «соглашение отрицательной логики»?
5. Что означают цифры, присутствующие в названии логического элемента?
6. Что такое таблица истинности и временная диаграмма? Правила их составления.
СОДЕРЖАНИЕ...
2. ФУНКЦИОНАЛЬНЫЕ СВОЙСТВА ПОЛНЫХ ДЕКОДЕРОВ
1. Цель лабораторной работы
Изучение функциональных свойств полных декодеров на примере ИМС серии КI55 и построение устройств на их основе.
2.Основные сведения
Полный декодер (DC) - комбинационная логическая схема (устройство), имеющая k входов, называемых "адресными", и N = 2k выходов. В любом случае сигнал активного уровня может быть только на одном из выходов, номер ("адрес") которого однозначно определяется комбинацией входных сигналов в текущий момент времени. Если выходы DC нумеровать десятичными числами, начиная с нуля, то адрес активизированного выхода можно определить, переведя двоичное k - разрядное число, отображающее комбинацию входных сигналов, в десятичную систему счисления. Для этого адресным входам присваивают весовые коэффициенты согласно "весам" разрядов двоичных чисел (2i, где i = {0, 1,…, k – 1} и соответственно их помечают. Число к называют "порядком" декодера. Если k=3, то это соответствует декодеру третьего порядка и у него будет N = 23=8 выходов. Выходы могут быть прямыми или инверсными, в зависимости от этого значение активного уровня для выходного сигнала меняется: если DC имеет инверсные выходы, то "активным" считается сигнал логического нуля (лог.0). В противном случае за активный уровень принимается сигнал логической единицы (лог.1).
сигнал логического нуля (лог.0). В противном случае за активный уровень принимается сигнал логической единицы (лог.1).
Реальные ИМС полного декодера имеют обычно дополнительные входы, называемые разрешающими или управляющими, сигналы по которым запрещают или разрешают активизацию выходов. На рисунке 1 приведены условные графические обозначения полных декодеров 3-го (рисунок 1,а) и 4-го (рисунок 1,б) порядков с прямыми и инверсными выходами, соответственно.
Для декодера D1 активным уровнем выходного сигнала будет лог.1, а для декодера D2 - уровень лог.0. Адресные входы помечены десятичными числами «1», «2», «4», «8» (согласно весовым коэффициентам разрядов двоичных чисел) и логическими переменными а0, а1, а2, а3, отображающими сигналы по адресным входам. Индекс у переменных аi соответствует показателю степени числа 2 при определении "веса" "адресного" входа и одновременно "веса" "адресной" переменной. Так, что а0 является адресной переменной самого младшего разряда, переменные а2 и а3 будут соответствовать 3-му и 4-му разрядам комбинации по адресным входам и являются переменными старших разрядов.
Таким образом двоичное число <а3 а2 а1 а0>, отображающие комбинацию значений адресных сигналов, укажет номер выхода с активным уровнем сигнала ("активизированный" выход).

a) б)
Рисунок 1 - Условные графические обозначения полных декодеров.
У декодера D1 один инверсный разрешающий вход, поэтому сигнал лог.0 будет активным и, и при наличии такого сигнала, на одном и выходов появится уровень лог.1. Например, при комбинации <а2 а1 а0> <110> на 6-м выходе DC будет сигнал лог.1, т.к. двоичное число 110(2) соответствует десятичному 6(10).
<110> на 6-м выходе DC будет сигнал лог.1, т.к. двоичное число 110(2) соответствует десятичному 6(10).
Функционирование полного декодера рис.1.а, можно описать следующей системой логических (булевых) функций:
_ _ _ _ _ _ _
у0 = S(а2 а1 а0); у4 = S(а2 а1 а0);
_ _ _ _ _
у1 = S(а2 а1 а0); у5 = S(а2 а1 а0);
_ _ _ _ _
у2 = S(а2 а1 а0); у6 = S(а2 а1 а0);
_ _ _
у3 = S(а2 а1 а0); у7 = S(а2 а1 а0).
 где уi - функции, определяющие значения выходных сигналов (I=0.7); S - логическая переменная, соответствующая сигналу на разрешающем входе; а конъюнкции вида (а2 а1 а0)i отображают комбинацию сигналов по адресным входам, при которой соответствующий выход будет активным (иметь сигнал лог.1). Эту комбинацию легко определить, если адресную
где уi - функции, определяющие значения выходных сигналов (I=0.7); S - логическая переменная, соответствующая сигналу на разрешающем входе; а конъюнкции вида (а2 а1 а0)i отображают комбинацию сигналов по адресным входам, при которой соответствующий выход будет активным (иметь сигнал лог.1). Эту комбинацию легко определить, если адресную переменную без знака инверсий заменить единицей, а со знаком инверсии - нулем. Например, конъюнкция (а2 а1 а0) соответствует комбинации а2 = 0,
переменную без знака инверсий заменить единицей, а со знаком инверсии - нулем. Например, конъюнкция (а2 а1 а0) соответствует комбинации а2 = 0,
а1 = а0 = 1, то есть <011>, и при S = 0, будет активизирован 3-й выход (у3=1). Аналогично, пользуясь системой (1), можно определить номер активного выхода при любой другой комбинации адресных сигналов.
Систему (1) можно записать в обобщенной форме:
 _ ~ ~ ~
_ ~ ~ ~
уi = S(а2 а1 а0) i, (2)
где i €{0,1,2,...7} - номер выхода полного декодера; множество конъюнкций (а2 а1 а0)i есть полное множество конституент логических функций от 3-х аргументов при их задании по единицам. Следовательно, полный декодер 3-го порядка с прямыми выходами можно рассматривать как "генератор" конституент логических функций 3-х аргументов и поэтому использовать для построения любых логических устройств (с 3-я входами).
Аналогично функционирование декодера D2 (рисунок 1,б) можно описать системой функций:
уi = (Sd ) (а3 а2 а1 а0) i, i €{0,1,2,...,15}, (3)
Так как выходы декодера инверсные (что отображено символом инверсии над правой частью выражения (3)), то сигнал активного уровня (лог.0) может появиться лишь при условии
_ _
S & d =1,
т.е. S = d = 0. Причем номер i активизированного выхода будет определяться комбинацией <а3 а2 а1 а0> i, существующей в данный момент времени на адресных входах DC. Множество {I} является полным множеством десятичных номеров конституент логических функций (4-х аргументов) при их задании по нулям. Следовательно, полный DC 4-го порядка можно использовать для построения любых логических устройств с 4 входами.
Обобщая выводы, полученные на основе выражений (2) и (3), можно доказать, что полные декодеры образуют функционально полный набор логических модулей, из которых можно построить любые логические устройства. При этом функциональная полнота сохраняется независимо от наличия разрешающих входов (их количества, указателей инверсий по этим входам и вида функций управления), а также независимо от указателей инверсий по выходам. Наличие же разрешающих входов расширяет функциональные возможности полных декодеров, так как их использованием можно реализовать дополнительно некоторые логические операции.
Для построения устройств на основе полных декодеров достаточно предусмотреть дополнительно логические элементы ИЛИ (либо ИЛИ-НЕ) - для декодеров типа D1, либо элементы И-НЕ (либо И) - для декодеров типа D2, В этом случае некоторая логическая функция F, описывающая устройство, может быть реализована по формулам (2):
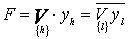 ; (4)
; (4)
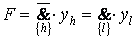 . (5)
. (5)
В формулах (4) и (5):
{h} - подмножество номеров "h" конституент, на которых F принимает значения; {l} - подмножество номеров конституент, на которых эта функция равна 0; V - символ дизъюнкции; & - символ конъюнкции. Причем между указанными подмножествами справедливы следующие соотношения:
 {h} V {l} = i и
{h} V {l} = i и  {h} Λ {l} = Ø (6)
{h} Λ {l} = Ø (6)
Здесь {I} есть полное множество номеров конституент функции F. Формула (4) справедлива, когда декодеры имеют прямые выходы, а (5) - для декодеров с инверсными выходами.
Следует отметить, что полный декодер, как универсальный логический модуль, позволяет реализовать "простые" логические функции. То есть может "выступать в роли" логических элементов, например, таких как НЕ, И, ИЛИ-НЕ и др. Обратитесь к системе функций (1). При S=0 имеем :
_ _ _ __________
у = a2 & a1 & a0 = a2 Λ a1 Λ a0- это функция ИЛИ-НЕ; а
у7 = а2 а1 а0 - это функция И и т.д. Но использование в таком качестве полных декодеров не эффективно.
2. Описание лабораторной установки
Эксперименты выполняются на субблоке ДЕШИФРАТОР типового лабораторного стенда. Условные графические обозначения декодеров приведены на лицевой панели стенда. В состав лабораторной установки входят следующие функциональные части:
- блок формирования адресных сигналов (БФС) на переключателях SА1, SA2;
- блок формирования разрешающих сигналов SA5, SA8;
- полный дешифратор (декодер) 3-го порядка;
- блок индикации (светодиоды HL, HL8).
БФС позволяет формировать сигналы, управляющие работой декодеров. Что позволяет создавать условия запрещающие или разрешающие работу декодеров.
В лабораторной установке исследуется функционирование дешифраторов двух типов: К155ИД4 и К155ИД7.
Упрощенные функциональные схемы коммутации стенда для выполнения лабораторных работ приведены на рисунке 2.


Рисунок 2. - Упрощенная функциональная схема субблока "ИD4"и "ИD7"
3. Задание на лабораторную работу
1.Ознакомиться с составом, назначением каждого функционального узла стенда. Уяснить расположение и назначение тумблеров, кнопок и светодиодов на лицевой панели стенда.
2.Исследовать работу дешифраторов в автономном режиме формирования адресных и управляющих сигналов.
3. Исследовать следующие режимы работы дешифраторов К155 ИD4:
- 2 дешифратора 2 х 4
- дешифратор 3 х 8
К155 ИД7: дешифратор 3 х 8.
Построить временные диаграммы работы стенда в указанных режимах.
4.Ознакомиться с назначением и цоколевкой микросхем К155 ИД4, К155 ИД7 и правилами формирования их условных графических обозначений (УГО).
5.Начертить функциональную схему полного дешифратора по УГО рисунок 1а и рисунок 1,б (вариант указывается преподавателем).
6.Построить функциональную схему на основе полного декодера, реализующую одну из функций, представленных в таблице 1 (вариант указывается преподавателем).
7.Сделать выводы по функциональному назначению и свойствах полных дешифраторов.
4.Методические указания
4.1.При уяснении назначения функциональных узлов стенда пользуйтесь схемами, приведенными на рисунке 2 и рисунке 3.
4.2.Определить разрешающие комбинации управляющих сигналов для исследуемых режимов.
4.3.Постройте временные диаграммы работы декодеров в исследуемых режимах.
4.4.Цоколевка - это нумерация выводов ИМС согласно типу корпуса, Уясните типы корпусов, исследуемых в лабораторном макете. Особое внимание обратите на номера выводов для подключения источника питания: общего провода и активного полюса (+5В).
Таблица 1 - Варианты индивидуальных заданий
| Вариант |
Название функции |
Микросхема |
Формула функции |
1 |
Сумма по mod2 |
К155 ИД4 |
Х = a mod2 b mod2 c |
2 |
Мажоритарность ≥2 из 3 |
К155 ИД4 |
Y = ab V ac V bc |
3 |
Инверсия суммы
по mod 2 |
К155 ИД7 |
______________
Z = a mod2 b mod2 c |
4 |
Логический порог |
К155 ИД7 |
_ _ _
W= abc V abc V abc |
5 |
Функция |
К155 ИД4 |
_ _ _ _ _ _
Q= abc V abc V abc |
6 |
Функция |
К155 ИД4 |
_ _ _
V= ab V bc V ac |
7 |
Функция |
К155 ИД7 |
_ _ _ _ _ _
U= ab V bc V ac |
Сопоставьте указатели по входам выходам УГО ИМС с действием входных сигналов и, соответственно, значением выходных сигналов функциональных элементов. Уясните метки в основном и дополнительных полях УГО согласно назначениях выводов ИМС и функции, реализуемой элементом. Приведите рисунки цоколевок ИМС К155 ИД4 и К155 ИД7.
При уяснении этих сведений руководствуйтесь ГОСТ 2.742-82. и справочными данными.
4.5.Чтобы составить функциональные схемы полных декодеров согласно УГО рисунка 1,а,б, руководствуйтесь логическими выражениями (1), (2) и (3) выходных функций соответствующего декодера и правилами построения функциональных схем по логическим выражениям. Учтите, что количество инверторов, необходимых для получения инверсий адресных сигналов, должно быть равно числу адресных входов.
Сопоставьте полученные схемы с аналогичными для ИМС ТТЛ, приведенными в справочниках. Сделайте выводы о результатах.
4.6.Чтобы построить функциональную схему, реализующую одну из функций таблиццы 1 с заданным типом декодеров, постройте карту Карно для этой функции. Затем, руководствуясь формулами (4) и (6) и изложенным в п.2 материалом, определите номера конституент этой функции и, в то же самое время, номера выходов декодера. Определите тип объединяющего элемента и постройте схему.
Результат предъявите преподавателю для проверки.
5.Содержание отчета
Отчет выполняется с требованиями кафедры АиПУ и должен содержать:
- Временные диаграммы согласно п.2 задания.
- УГО и цоколевку ИМС К155 ИД4 и К155 ИД7.
- Функциональные схемы по п.5 и п.6 задания.
- Выводы по выполненной работе.
Контрольные вопросы
1.Что такое "полный декодер" и его "порядок"?
2.Как ИМС К155 ИД4 использовать в качестве полного декодера третьего порядка? Начертите схему и пронумеруйте выходы.
3.Каким образом можно найти систему логических функций, описывающий полный декодер 2-,3- и 4-го порядка?
СОДЕРЖАНИЕ...
3. МУЛЬТИПЛЕКСОРЫ - СЕЛЕКТОРЫ
1. Цель лабораторной работы
Изучение и экспериментальное исследование функциональных свойств мультиплексоров - селекторов (MS) в реализации булевых функций и применения ИМС МS.
2. Основные сведения и понятия
Мультиплексор - селектор - это электронный коммутатор дискретных сигналов с нескольких «направлений» на одно. Обычно МS имеет две группы входов: одну из «к» входов, называемых адресными или управляющими, и другую – из 2к входов, называемых информационными. Комбинация сигналов на адресных входах однозначно указывает номер («адрес») информационного входа, который будет «подключен» к выходу в рассматриваемый момент или интервал времени.
Число «к» принято называть «порядком» мультиплексора - селектора (в дальнейшем просто «мультиплексор» или МS) Порядок МS предопределяет «способность» его к коммутации определенного количества информационных входов и функциональные возможности микросхем МS.
По принципу действия MS - это комбинационное устройство, значение выходного сигнала которого однозначно определяется значением информационного, скоммутированного в данный момент времени к выходу мультиплексора.
По - существу MS образован полным декодером k-того порядка и многовходовым логическим элементом 2И-2к ИЛИ либо 2И-2к ИЛИ-НЕ. На один из входов элемента 2И подается информационный сигнал, а на другой сигнал с одного из выходов полного декодера. Таким образом, в каждый рассматриваемый момент времени может быть скоммутирован только один из информационных входов, а выходной сигнал МS быть инверсным либо совпадать со значением входного информационного сигнала.
Реальные ИМС мультиплексоров имеют ограниченное число информационных входов: 4, 8 или 16 (к=2, 3 или 4) и дополнительно, кроме информационных и адресных, так называемый «разрешающий» вход или вход «разрешения/запрета». Сигнал по этому входу запрещает или разрешает коммутацию информационных входов. В состоянии запрета выходной сигнал МS принимает фиксированное значение и не зависит от значений информационных и адресных сигналов. Кроме того, есть мультиплексоры с двумя выходами - прямым и инверсным. Так на рисунке 1 показано условное графическое обозначение (УГО) мультиплексора - селектора третьего порядка (МS-3), имеющего 8 информационных выходов, помеченных групповой меткой D, три адресных входа с групповой меткой SED, один инверсный вход разрешения работы Е и два выхода.

Рисунок 1. - УГО мультиплексора - селектора третьего порядка
Если на входе разрешения Е сигнал равен логической единице (лог.1), то независимо от других сигналов на прямом выходе будет постоянно сигнал логического нуля (лог.0), а на инверсном - лог.1.
Если поставить входным сигналам мультиплексора в однозначное соответствие логические переменные: х-, х1, . . .х 7 - информационные; а0, а1, а2 – адресные и «Е» - разрешение, то логическое выражение (функция), показывающее зависимость выходного сигнала от входных, будет иметь вид:
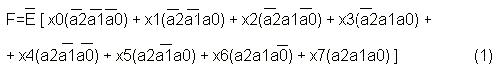
где символ «+» означает логическое сложение (дизъюнкцию); выражения в круглых скобках соответствуют логическому произведению (конъюнкции) адресных переменных, взятым со знаком или без знака инверсии - черта над переменной.
Выражение (1) описывает сигнал на прямом выходе мультиплексора третьего порядка (МS-3) и является его логико-математической моделью. Если использовать символ V групповой дизъюнкции, то (1) можно представить в сокращенной форме:
_ i=7
F = E * V xi(a2 a1 a0)i , i € {0,1,2,...,7} (2)
i=0
При Е=0, что соответствует состоянию «разрешения» коммутации, выражение (2) представляет собой дизъюнкцию по всему множеству {i} номеров конституент логических функций, аргументами которых являются адресные переменные мультиплексора. Конъюнкции вида (а2а1а0)i отображают комбинацию сигналов по адресным входам, при которой i-й вход и соответствующая ему переменная хi будут «скоммутированы» к выходу МS.
Из анализа приведенных выражений очевидно, что MS является функционально полным логическим элементом. Поэтому, с его помощью можно реализовать логическую функцию любой сложности. Существует два способа реализации. В первом количество аргументов реализуемой функции совпадает с порядком мультиплексора, во втором порядок мультиплексора выбирается меньшим, чем число функциональных аргументов.
Рассмотрим первый способ реализации логических функций.
Для этого необходимо определить номера конституент (и номер информационных входов МS), на которых функция принимает значение лог.1 либо лог.0, а затем выполнить соответствующие подключения информационных входов МS к шинам лог.1 и лог.0. При этом на адресные входы следует подавать сигналы, соответствующие аргументам реализуемой функции.
К информационным входам подключаются константы: «лог.0» или «лог.1». Номера информационных входов для подключения констант выбирают из подмножеств {h} и {l}. Определить данные подмножества проще всего по маскирующим матрицам мультиплексоров путем «наложения» карты Карно реализуемой функции на маскирующую матрицу. При этом названные матрицы и карты Карно должны быть одного «порядка».
Последовательность подачи входных сигналов на адресные входы мультиплексора определяется как соответствие аргументов реализуемой функции адресным переменным тоже по результату наложения. На рисунке 2(а,б) приведены маскирующие матрицы МS-3 и MS-4, соответственно.
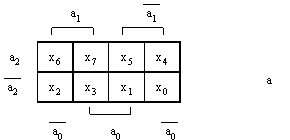
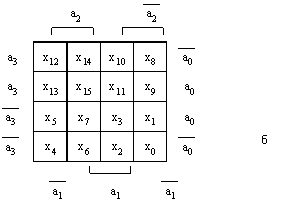
Рисунок 2. – Маскирующие матрицы мультиплексора 3-го порядка (а) и четвертого порядка (б).
В качестве примера рассмотрим реализацию функции от трех аргументов:
_ _ _ _ _
F = abc V abc V a bc V a b c. Карта Карно для данной функции приведена на рисунке 3.
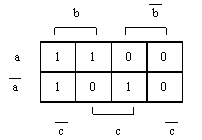
Рисунок 3. Карта Карно для функции F.
Так как реализуемая функция зависит от трех аргументов, то потребуется мультиплексор 3-го порядка, например К155КП7 (см. рисунок 1). По результату наложения карт Карно (рисунок 3) на маскирующую матрицу (рисунок 2, а) определяем:
{h} = {1,2,6,7}; {I} = {0,3,4,5}: (3)
а0 = с; а1 = b; а2 = а (4)
Номера, входящие в подмножества {h} и {l}, находятся как перечень индексов информационных переменных , стоящих в клетках маскирующей матрицы, приходящихся на клетки карты функции со значениями лог.1 и лог.0, соответственно. Маскирующая матрица МS вычерчивается в форме карт Карно для функций, аргументами которых являются адресные переменные мультиплексора, и показывает, какие информационные переменные xi будут скоммутированы при рассматриваемой комбинации адресных переменных. Равенства (4) определяют по разметке маскирующей матрицы и карты функции. Они предписывают порядок подачи сигналов, отображаемых аргументами функции, на адресные входы мультиплексора.
Принципиальная схема, реализующая названную функцию на мультиплексоре К155КП7, приведена на рисунке 4.

Рисунок 4. Принципиальная схема реализации функции F на мультиплексоре 3-го порядка.
Рассмотрим второй способ реализации логических функций.
В качестве примера возьмем ту же функцию. Поэтому будем использовать карту Карно, представленную на рисунке 3. Функцию реализуем на мультиплексоре 2-го порядка. Его маскирующая матрица приведена на рисунке 5.
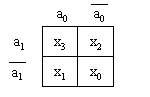
Рисунок 5. Маскирующая матрица мультиплексора 2-го порядка.
Поскольку, количество адресных входов мультиплексора и аргументов функции не совпадает, то необходимо выбрать часть аргументов, которые будут поданы на адресные входы мультиплексора. Оставшиеся аргументы должны быть определенным образом подключены к информационным входам, при этом допускается использование дополнительных логических элементов. Сопоставление адресных входов мультиплексора и аргументов функции осуществляется при инициализации карты Карно и маскирующей матрицы. После этого порядок подключения аргументов менять нельзя, это не позволит реализовать функцию.
Далее производится наложение маскирующей матрицы на карту Карно. Поскольку количество клеток в них не одинаково, то одна клетка маскирующей матрицы будет покрывать несколько клеток карты Карно. Назовем эту совокупность областью. Количество клеток во всех областях должно быть одинаково. Результат наложения представлен на рисунке 6.
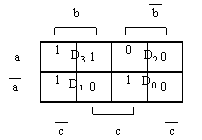
Рисунок 6. Наложение маскирующей матрицы на карту Карно.
Каждую область можно рассматривать как самостоятельную карту Карно. Поэтому дальнейшая минимизация проводится в каждой области отдельно. Аргументами, участвующими в минимизации являются те, которые должны быть подключены к информационным входам мультиплексора. В данном примере это единственный аргумент «С». Из рисунка 6 видно, в области D0 функция равна 1 только при С=1, в области D1 – только при С=0, в области D2 при любом значении С функция равна 0 и в области D3, вне зависимости от С, функция равна 1. Отсюда определяется вид функций схемы реализации которых должны быть подключены ко входам Di.:
_
D0 = С; D1 = C ; D2 = 0; D3 = 1.
На рисунке 7 приведена принципиальная схема реализации данной функции на мультиплексоре 2-го порядка.

Рисунок 7. Принципиальная схема реализации функции F на мультиплексоре 2-го порядка.
3. Состав лабораторной установки
Лабораторная работа выполняется на субблоке мультиплексоры унифицированного лабораторного стенда.
Функциональные свойства МS изучаются на примере микросхем К155КП2 и К155КП7, представляющих собой, соответственно, мультиплексор-селектор 2-го порядка (сдвоенный) и МS-3.
Для задания сигналов по информационным входам служат тумблеры SA1÷SA8 и коммутационные гнезда "+" и "". Путем коммутации этих гнезд со входами можно задать функциональные значения сигналов по каждому информационному входу мультиплексоров.
4. Задание на лабораторную работу
Уяснить цели работы, методы исследования и состав лабораторной установки.
- Исследовать работу мультиплексоров в статическом режиме при реализации заданных в таблице1 функций (по индивидуальному заданию).
- Исследовать работу мультиплексоров в динамическом режиме при реализации последовательности импульсов с заданными временными соотношениями.
Сделать обобщающие выводы по применению МS в статическом и динамическом режимах работы.
5. Методические указания
5.1. Функциональные свойства МS - это способность их к реализации логических функций и к формированию последовательностей сигналов.
Изучение функциональных свойств МS в статическом режиме, когда входные и выходные сигналы имеют установившиеся значения, ведется аналитическим методом (по логико-математическим моделям). В динамическом режиме, при периодическом изменении входных сигналов, используется метод временных диаграмм, показывающих изменение во времени значений выходных сигналов в зависимости от последовательностей входных.
5.2. Функциональные свойства МS в статическом режиме исследуется на примерах реализации логических функций, описывающих работу комбинационных устройств: цифрового компаратора и арифметического сумматора двух 2-разрядных двоичных чисел; мажоритарных элементов; схем логического порога и схем контроля четности-нечетности (см. Таблицу 1) Номер варианта индивидуального задания указывает преподаватель либо на бригаду либо каждому студенту отдельно.
Индивидуальным заданием предусматривается:
- по наименованию функции определить ее значения в зависимости от аргументов, т.е. значения выходного сигнала от значений входных сигналов;
- построить карту Карно этой функции;
- выбрать порядок мультиплексора и соответствующую микросхему.
- выбрать способ формирования сигналов по адресным входам и, подавая эти сигналы, проконтролировать значения сигнала на выходе мультиплексора.
При выполнении заданий (варианты 1÷5) учтите, что выходы у компаратора и сумматора функционально не равнозначны. Поэтому порядок передачи сигналов на эти входы жестко фиксирован, а сами сигналы и входы имеют определенное функциональное значение. Так как обрабатываемые числа 2-разрядные, то для их представления требуется по паре логических переменных:
- для числа А - <а1а0>;
- для числа В - <b1b0>.
Переменным а0, b0 будут соответствовать младшие, а переменным а1,b1 - старшие разряды чисел. Тогда наборы <а1а0> и <b1b0> будут отображать значения чисел А и В, соответственно. Если условия А=В, А>В, А<В выполняются, то выходные сигналы, описываемые функциями R, B, M, должны принимать значения лог.1. Аналогично для арифметического сумматора: если сумма вторых разрядов равна 1 или возникает сигнал переноса, то функции S2 и Р3 должны иметь значение лог. 1.
Таблица 1 - Варианты индивидуальные задания
№ |
Реализуемая функция |
Обозначение функции |
Компаратор 2-разрядных двоичных чисел: |
1 |
"Равно" (А = В) |
R |
2 |
"Больше" (А > В) |
B |
3 |
"Меньше" (А < В) |
M |
Арифметический сумматор 2-разрядных
двоичных чисел: |
4 |
- второй разряд суммы |
S2 |
5 |
- сигнал переноса в 3-й разряд |
P3 |
6 |
Мажоритарность "≥2 из 3" |
X |
7 |
Логический порог "=2 из 4" |
V |
8 |
Контроль четности / нечетности 4-х сигналов |
W |
9 |
Сложение по модулю 2 трех аргументов |
Mod 2 |
10 |
_ _ _ _ _ _
Функция U= ab V bc V ac |
U |
Задания 6?10 относятся к реализации (с числом входов >2) логических элементов, у которых все входы логически равнозначны, поэтому порядок подачи многовходовых сигналов на адресные входы МS безразличен.
Эксперименты провести на подтверждение адекватности функционирования исследуемой схемы включения мультиплексора описываемой функции. Для этого сопоставьте значения выходного сигнала МS со значением функции при всех комбинациях по адресным входам.
5.3. Выводы о применении мультиплексора сделайте, отметив:
а) прямое назначение и существующие виды МS (не только в серии К155);
б) возможность реализации логических функций и комбинационных схем на МS без дополнительных элементов;
в) возможности формирования импульсных последовательностей с заданными соотношениями длительностей импульсов и пауз в составе более сложных устройств.
Делая выводы (а), учтите, что в интегральном исполнении выпускаются мультиплексоры, различающиеся не только количеством информационных и адресных входов, т.е. порядком, но и способом организации выходов.
Формулируя выводы (б), оцените множество логических функций, которые можно реализовать на мультиплексоре-селекторе в зависимости от его порядка. Назовите свойства реализованных устройств.
5.4. Содержание отчета.
Отчет оформляется согласно требованиям, принятым на кафедре АиПУ, и должен содержать:
1. цели лабораторной работы;
2. функциональную схему реализации заданной логической функции, согласно таблицы1;
3. выводы по результатам выполнения лабораторной работы.
6. Вопросы для самопроверки
1. Почему мультиплексоры-селекторы можно отнести к универсальным логическим модулям? Докажите это.
2. Что называют порядком мультиплексора-селектора? В чем целевое назначение МS? Назовите разновидности ИМС мультиплексоров.
3. Каким образом по алгебраическому выражению булевой функции ее можно реализовать на ИМС МS? Ответ иллюстрируйте примером.
4. Сколько логических функций можно реализовать на мультиплексоре К155КП1в виде устройства с типовой структурой?
5. Каковы этапы построения комбинационных устройств типовой структурой на мультиплексорах? Приведите пример.
6. Каким образом мультиплексор-селектор можно использовать для формирования последовательностей импульсов? Нарисуйте функциональную схему и объясните ее работу, построив временные диаграммы для конкретной последовательности.
7. Какие ограничения накладываются на формирование импульсных последовательностей с помощью МS? (На длительность цикла, импульсов и пауз, их число.)
СОДЕРЖАНИЕ...
ЛИТЕРАТУРА
1. Цифровые устройства и микропроцессорные системы. Калабеков Б.А.– М.: Радио и связь 1997.
2. Аналоговая и цифровая электроника: Учебник для вузов/ Ю.Ф. Опадчий, О.П. Глудкин, А.И. Гуров; Под ред. О.П. Глудкина. – М.: Радио и связь, 1996.
3. Цифровые интегральные микросхемы. Справочник .П.П. Мальцев, Н.С. Долидзе, М.И. Критенко и др. - М.: Радио и связь, 1994.
4. Популярные цифровые микросхемы: Шило В.Л.Справочник. – М.: Радио и связь, 1988.
5. Цифровые интегральные микросхемы: Справочник/ М.И. Богданович, И.Н. Грель, С.А. Дубина и др. Мн.: Беларусь, Полымя, 1996.
6. Логические ИС КР1533, КР1554. Справочник/ И.И. Петровский, А.А. Троян, В.С. Чувелев. М.: БИНОМ, 1993.
Используются технологии
uCoz