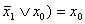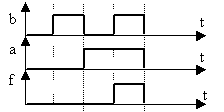
Рис. 1. Временная диаграмма функции «И»
Основными операциями булевой алгебры является:
- логическое сложение – операция ИЛИ, дизъюнкция. Справедлива для любого числа переменных, соответствует математической операции объединения множеств. (табл.истинности)
- логическое умножение – операция И, конъюнкция справедлива для любого числа переменных соответствует операции пересечения множеств (табл.истинности)
- отрицание – инверсия или дополнение. Для обознач. исп.черту. Выражается в следующем:
если a=1, a=0,
a=0, a=1,
Операции Λ и V обладают рядом свойств, сходных со свойствами обычных математических операций:
Сочетательный закон х1(х2х3)=(х1х2)х3
x1V(x2Vx3)=(х1Vx2)Vх3
Переместительный закон х1?х2=х2?х1
х1Vх2=х2Vх1
Распределительный закон х1(х2Vх3)=х1х2V х1х3
х1V (х2х3)=(х1Vх2)V(х1Vх3)
? и V равнозначные, нет приоритетов.
Кроме данных законов существует ряд теорем булевой алгебры:
- хV0=х хΛ1=х
- хV1=1 хΛ0=0
- хVх=х хΛх=х
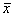 Vх=1
Vх=1 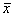 Λх=0
Λх=0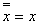
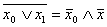
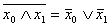 - преобразование Де-Моргана
- преобразование Де-Моргана- х0хVх0=х0 (х0Vх1)х0=х0
- х1
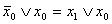 (х1V
(х1V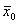 )х0=х0х1
)х0=х0х1
- х1х0V
 (х1Vх0)(
(х1Vх0)(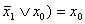
Возвращаемся к ФАЛ. Уже говорили, что для 2ух аргументов может составить 16 функций:
Составим таблицу истинности для них
f0(x1x2)=0 f15(x)=1
f3(x1x2)=x1 f5(x1x2)=x2 - вырожденные – НЕ зависят от аргументов
f1(x1x2)=x&x2(?)- конъюнкция, логическое сложение, лог «И»
f2(x1x2)=(x1*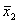 )=x1Λх2 – запрет, отрицание импликации, читать х1 запрет по х2
)=x1Λх2 – запрет, отрицание импликации, читать х1 запрет по х2
f4(x1x2)=(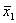 *х2)=х2 Λх1- х2 запрет по х1
*х2)=х2 Λх1- х2 запрет по х1
f6(x1x2)=x1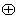 x2 – сумма по модулю 2, сумма без переноса
x2 – сумма по модулю 2, сумма без переноса
f7(x1x2)=x1Vx2 дизъюнкция, лог. ИЛИ
f8(x1x2)=x1vх2 =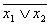 лог. ИЛИ-НЕ, отрицания дизъюнкции, стрелка Пирса, функция Вебба
лог. ИЛИ-НЕ, отрицания дизъюнкции, стрелка Пирса, функция Вебба
f9(x1x2)=x1~x2 эквивалентность, функция равнозначности х1 и х2
f10=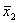 ; f12=
; f12=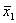 - инверсия, отрицание
- инверсия, отрицание
f11=x2>x1=x1V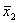
f13= x1>x2=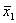 Vx2 – импликация , если х2, то х1. х1 влечет х2
Vx2 – импликация , если х2, то х1. х1 влечет х2
f14 =x1|x2=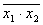 - лог. И-НЕ, шрих Шеффера, отрицание конъюнкции.
- лог. И-НЕ, шрих Шеффера, отрицание конъюнкции.
Имея логические элементы, осуществляющие элементарные операции f0?f15 можно выполнить логическую операцию любой сложности.
Функционально полной системой или базисом называется совокупность логического элемента, позволяющая реализовать логическую схему любой сложности.
Условие наличия 16 различных типов логических элементов, реализующих одну из 16 функций f0÷f15является достаточным условием для синтеза логического устройства любой сложности, но не является необходимым условием.
Последовательно исключая из базиса функции можно получить минимальный базис.
Под минимальным базисом понимают такой набор функций, исключения из которого любой функции превращают этот набор в неполную систему функций.
Возможен выбор различных минимальных базисов, различающихся числом входящих в них функций. Выбор базисов определяется экономическими и техническими показателями.
Для определенных способов получения минимального базиса необходимо рассмотреть 5 свойств алгебры логики:
- Сохранение 0: Функция f(x1,...xn) обладает этим свойством если f(0,…0)=0 т.е. функция на нулевом наборе аргументов = 0.
- Сохранение 1: f(1,..1)=1
- Самодвойственность : т.е. инвертирование всех аргументов приводит к инверсии значения функции: f(
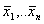 )=
)=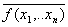 .
.
- Свойство монотонности: если значения функции не убывают при переходе от любого набора значений аргумента к любому другому возможному набору, в котором значения соответствующих аргументов не меньше чем в 1-ом наборе, при
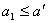 ;
; 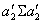
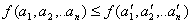 или f(0,0)≤f(0,1) ≤f(1,0) ≤f(1,1).
или f(0,0)≤f(0,1) ≤f(1,0) ≤f(1,1).
- Свойство линейности: функция линейна , если ее можно представить в следующем виде f(1,1)=f(0,0)
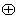 f(0,1)
f(0,1)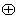 f(1,0) т.е. функция на единичном наборе равно сумме по модулю 2 значений функции на всех других наборах.
f(1,0) т.е. функция на единичном наборе равно сумме по модулю 2 значений функции на всех других наборах.
Рассмотрим наличие свойств в каждой элементарной функции
Система функций будет полной (образует базис), если для любых из 5 рассмотренных свойств в этой системе найдется хотя бы одна функция, не обладающая этим свойством.
- Функция И (f1) не обладает самодвойственностью и линейностью, в систему надо включить функцию, не обладающую остальными свойствами. В качестве такой функции может быть выделена НЕ (f10) или (f12)
- ИЛИ+НЕ f7+[f10 или f12]
- ИЛИ-НЕ f8=x1↓x2
- И-НЕ f14=x1|x2
- Функция запрета f4=x1Δx2 обладает лишь свойством сохранения 0. Для создания полной системы логических функций необходима функция, лишенная данного свойства.
В качестве такой может быть выбрана константа 1 на х2 f15 или др.(fд÷f15)
Вернутся к содержанию...

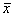 Vх=1
Vх=1 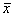 Λх=0
Λх=0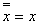
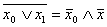
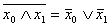 - преобразование Де-Моргана
- преобразование Де-Моргана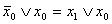 (х1V
(х1V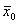 )х0=х0х1
)х0=х0х1 (х1Vх0)(
(х1Vх0)(